(G S Manku, email: manku.gs@gmail.com)

(10.1).1 General

A solution is a homogeneous mixture of two or more chemical substances at the molecular level. The composition of a solution of solutions may vary within certain limits and may be regarded as a molecular dispersion of substances within each other.

The chemical component present in smaller amounts is regarded as solute and the component present in larger amounts is termed as solvent. The terms solute and solvent are interchangeable. In a 15 % acetone – 85 % water mixture, acetone is solute present in water as solvent, whereas in 85 % acetone – 15 % water mixture, water becomes the solute present in acetone as solvent.

Generally, there is a limit to solubility of solutes in a solvent called the solubility of the solute. When a small amount of solute is added to a solvent, on stirring, it gives a clear solution. Once the limit is reached, addition of further solute will lead to a state where there is equilibrium between undissolved solute and dissolved solute. The solution is such a state is called a saturated solution.

A solution having water as solvent is called an  aqueous solution. This may have ionic species derived from the solute, or covalent molecules dissolved with (carbon dioxide, ammonia, ethanol, acetone, hydrogen cyanide, etc.) or with partial or almost complete ionization (hydrogen chloride, hydrogen fluoride, nitric acid, acetic acid, etc.).

The different solutes have a wide range of solubility, for which, presently, a foolproof explanation is npt available.

(10.1).2 Effect of Temperature on Solubility

The dissolution of a solute in a solvent is analogous to melting process. In the melting process, the thermal and vibration energy of the constituent particles (ions or molecules) of the solid,  arranged in a particular lattice structure, exceeds their lattice energy. This results in free movement of the particles, the lattice breaks and the solid melts. Similarly, in the dissolution process, the solvent molecules attract the constituent particles of the solid, generally through ion–dipole or dipole–dipole attractions. This results in weakening of the interlattice forces. As the interlattice forces weaken, the constituent particles of the solute spread around in the solvent (where they can move freely). A solution is formed.

In general, solutes with high melting point (having high lattice energy) have a low solubility.

It is therefore expected that the solubility of the solutes will increase with increase in temperature. Different types of forces are involved in the dissolution process.

1. Thermal (kinetic) energies: At higher temperatures, the higher vibration energies of the constituent particles weaken the lattice forces.
2. Electrostatic Energies: Ionic solutes dissolve more readily in polar solvents than in nonpolar solvents as in polar solvents, the ion–dipole interactions are more due to ion–ion interactions. In nonpolar solvents, ionic solutes dissolve due to much weaker ion–induced pole interactions and have a low solubility because of the resulting low solvation energy.
3. Chemical energies: There may be specific solute–solvent chemical interactions at different levels. For example CaCl­₂.2H₂O dissolves in eater forming hydrated [Ca(H₂O)_x]²⁺ and [Cl(H₂O)_y]^–

The term solvation energy includes both the all the different types of energies.

(10.1).3 Solubility Curves

The plots of solubility of a solute in a solvent at different temperatures are called the solubility curves of the solutes. Three types of solubility curves are observed.

1. Usually, these are smooth curves with a positive slope [potassium nitrate, curve (c), Figure 11.1.1].
2. A break in solubility curve [potassium nitrate, curve (b), Figure 11.1.1] is observed whenever the solute forms different hydrates in aqueous solutions (which are stable at different temperatures), so that nature of the solid in equilibrium with the solution changes with temperature, for example, sodium sulphate, which exists as Na₂SO₄.10H₂O at lower temperatures and as Na₂SO₄ at higher temperatures.
3. Sometimes, the solubility decreases with increase in temperature [sodium chloride, curve (a), Figure 11.1.1]. This is usually due to a change in the chemical structure of the solute at different temperatures.

Figure 11.1.1 Solubility curves of (a) sodium sulphate,
(b) potassium nitrate and (c)  sodium chloride

(10.1).4 Role of Water as Solvent 

When an ionic solute is placed in water, ion–dipole interactions take place and the water molecules align along the surface of the solid. Their negatively charged oxygen ends are towards the cations and the positively charged hydronium (proton) ends are towards the anions. Due to the electrostatic attractions between the opposite charges at the surface, the inter-ionic attractions in the solid lattice are weakened. Some of the surface ions get pulled away by the solvent (due to the thermal vibration energies) as hydrated ions and form a solution. Generally, ionic solutes have a greater solubility in the solvent with higher dielectric constants.

(10.1).4.1 Hydrogen bonding and Solubility in water

There is a strong hydrogen bonding in water. In order to be soluble in water, the solute must weaken these hydrogen bonds. The extent to which the solute can weaken the hydrogen bonds present in water and form stronger ion –dipole bonds, determines the solubility in water.

The nonpolar solutes are not able to break the hydrogen bonding in water as they cannot form strong bonds with water molecules and get ‘squeezed out’, i.e., they do not go into solution to any appreciable limit.

This is true of other hydrogen bonded solvents also.

(10.1).4.2 Solubility of Long-Chain Molecules with Polar Ends

Long-chain aliphatic alcohols, amines or carboxylates have a nonpolar hydrophobic carbon chain and a polar end which can form strong hydrogen bonding water. When these compounds are placed in water, they are swept to the surface in such a way that their polar ends are in water and the nonpolar ends are above the surface (Figure 11.1.2). In this way, a uni-molecular film is obtained on the surface.

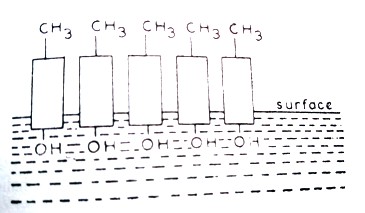
Figure 11.1.2 Pictorial representation of dissolution of
polar ends of long-chain forming uni-molecular layer
of the solid above the surface of water.

Such solids find application in covering the liquid surface with unimolecular layers

(10.1).4.5 Chemical Structure and Solubility

(10.1).4.5.1 Chemical Structure and Solubility

Like dissolves like is a familiar rule applicable to the solubility of the solutes with respect to chemical structure and dipole nature of solvent. Thus, paraffins dissolve readily in benzene – both are hydrocarbons but polyhydric sugars are water soluble and insoluble in benzene.

Though rigid rules regarding solubility of the solutes in terms of size, charge and electronic structure of ions and compounds cannot be framed, some generalizations can, however be made.

1. Due to lower lattice energy, large ions form more soluble compounds. For example, cesium iodide (ionic radii of Cs⁺ = 169 pm, I ^– = 216 pm, lattice energy U = – 583 kJ mol ^–1) is ten times more soluble than sodium fluoride (Na⁺ = 85 pm, F ^– = 136 pm, lattice energy U = – 892 kJ mol ^–1).
2. Higher ionic charge density lowers the solubility in aqueous and polar solvents. Thus, BaO is 2000 times more soluble than MgO. (ionic radii of Mg²⁺ = 85 pm, Ba²⁺ = 135 pm, O^2– = 140 pm,  lattice energy U for MgO =  – 3.93 mJ mol^–1, BaO = – 747 kJ mol ^–1).
3. If one of the ions in an ionic solute has a very small size compared with the other ion, a tightly packed lattice cannot be formed and this leads to a lowering of lattice energy. Thus out of magnesium sulphate and barium sulphate, using generalizations (2) above, barium sulphate should be more soluble in water as Ba²⁺ ions have a lower charge density. Actually, reverse is true. This is because, small sized Mg²⁺ ion cannot form a closed packed lattice with very large sized sulphate ions (ionic radius = 296 pm) (ionic ratio of cation to anion in magnesium sulphate is 0.26, in barium sulphate, it is 0.51;  for a stable octahedral lattice, the ionic radius ratio should be between 0.414 and 0.73). Hence, magnesium ion gets hydrated, becomes larger sized cation and then forms a stable solid lattice. Due to the presence of water molecules within the crystal structure, the inter-ionic attractions are decreased resulting in lowering of lattice energy, Hence, magnesium sulphate (MgSO₄.7H₂O) becomes more soluble as compared to barium sulphate (BaSO₄),
4. Polarization of Ions in the Crystals: Polarization of anions by the cations leads to covalent bonding. Hence, solubility of the compound decreases. For example, solubility of silver halides decreases from silver fluoride (soluble) to silver iodide (insoluble) due to increasing polarization of the larger sized anions by small sized Ag⁺ ions (121 pm). In fact, silver iodide is a covalent compound with zinc blende structure.

(10.1).5.2 Solubility from Chemical Reactions

In solution of paraffins (alkanes) in petrol, the solute retains its molecular character, whereas dissolution of say, zinc fluoride in hydrochloric acid, is clearly due to a chemical reaction:

ZnF₂ + 2HCl → ZnCl₂ + 2HF

Between these two extremes of solution, dissolution of solutes may involve gradual transition from physical to chemical process without a clear-cut demarcation.

Dissolution of sodium chloride in water is clearly a physical process as crystallization of the solution obtained gives the original solute. Dissolution of sodium chloride in water is clearly a physical process as crystallization of the solution obtained gives the original solute. Dissolution of anhydrous sodium carbonate in water or copper sulphate in dilute sulphuric acid gives a clear solution, which upon crystallization, gives the hydrated salts of original solutes (Na₂CO₃.10H₂O or CuSO₄.5H₂O). However, these processes do not involve any chemical change in the properties of the solute and are also regarded as a normal solution formation.

However, dissolution of metals in acids or alkalis, of solutes in sulphuric acid, etc. generally involve chemical reactions. Chemical reactions which help dissolution may be of acid–base or redox reactions:

Na₂O + H₂O →  2NaOH             (Solution of Na₂O in water)
Na₂O + H₂O →  2Na⁺  + OH ^–      (Solution of Na₂O in water)
Al(OH)₃ + 3HCl → Al³⁺ + 3Cl^– + 3H₂O
(Solution of Al(OH)₃ in alkali)
Zn(OH)₂ + 2OH^– → ZnO₂^2– + 3H₂O  (Solution of Zn(OH)₃ in alkali)
Zn(OH)₂ + 2HCl → Zn²⁺ + 2Cl^– + 2H₂O
(Solution of Zn(OH)₂ in acids)
Ca₃(PO₄)₂ + 6H⁺ →  3Ca²⁺ + 2H₃PO₄
 (Solution of Ca(PO₄)₃ in acids)
2Al + 2H₂O + 2OH^– → 2AlO₂^–   + 3H₂  (Solution of Al in alkali)
3HgS + 2NO₃^–  + 8H⁺ → 3Hg²⁺ + 3S + 2NO + 4H₂O
(Solution of HgS in HNO₃)

These processes cannot be classified as dissolution as upon crystallization of the solution obtained by evaporation, original solute cannot be recovered.

(10.1).6 Energy Changes in Solution Formation

(10.1).6.1 Hydration and Lattice energies

The difference between the solutions of nonpolar solutes in nonpolar solvents and mixing of ideal gases chiefly due to weak solute–solvent and solute–solvent interactions. In these cases, the free energy change ΔG for the dissolution will be due to the entropy changes (ΔS) only

ΔG = ΔH – TΔS =  – TΔS    (as ΔH = 0)

As for ideal gases, for mixing, if x₁ and x₂ are the mole fractions of the solute and solvent,

ΔS = – R(x₁ ln x₁ + x₂ ln x₂)
And,  ΔG =    – RT(x₁ ln x₁ + x₂ ln x₂)

At 298 K, the free energy of mixing is small, maximum value of free energy mixing released [being at δ(ΔG/ δ (x₁) = 0] is at x₁ = 0.5, and is – 2  8.314  298  0.5 log 0.5 =  172 J mol ^–1  or 1.72 kJ mol^–1 only.

(10.1).6.2 Effect of Complex Formation

Many solutes dissolve in solvents due to complex formation. Examples of solvent extraction of metal complexes into organic solvents demonstrate this phenomenon. Most familiar is the extraction of nickel(II) into dimethylglyoxime (HDMG) solutions of chloroform:

Ni²⁺ + 2(H DMG) → [Ni(DMG)₂] + 2H⁺

Even in aqueous solutions, many substances dissolve due to complex formation:

SnC₂O₄  + C₂O₄^2–⇌ [Sn(C₂O₄)₂]^2–
AgCl + Cl^– ⇌ [AgCl₂] ^–
CuCl + 2KCN ⇌ [Cu(CN)­₂] ^– + 2K⁺ + Cl^–
Cr(OH)₃ + 3OH^– ⇌ [Cr(OH)₆]^3-
CaHPO₄ + H₂Y^2– ⇌ [CaY]^2–  + H₃PO₄   (Y = EDTA)

In these cases also, the original solute does not get crystallized out from the solutions obtained.

The dissolution of the solute can be considered in terms of a Born – Haber cycle. The overall enthalpy of solution, ΔH_soln is the sum of the enthalpy of dissociation of the solid into gaseous ions by giving lattice energy U to the system and enthalpy of dissolution of the gaseous ions releasing the hydration enthalpy of the solution ΔH_solv:

M⁺A^–(s) →  M(g)⁺  + A(g)^–                  ΔH = – U
 M(g)⁺  + A(g)^– + solvent  → M(solv)⁺ + A(solv) ^–   ΔH =  ΔH_solv
Adding. M⁺A ^– + solv → M(solv)⁺ + A(solv) ^–   ΔH_soln = – U + ΔH_solv

ΔH_soln depends on

1. Ability of solvent to coordinate with the ions through ion–dipole interactions, and
2. Type and size of the ions.

The lattice energy depends upon the type and size of the ions. The ion–ion interactions are definitely stronger than ion–dipole interactions, and are comparable to the lattice energy. Hence, ΔH_soln  is a delicate balance of lattice energy and the solvation energy of ions, and can be either positive or negative.  If ΔH_soln is positive, cooling occurs during dissolution. But if ΔH_soln term is highly positive, the entropy changes (T ΔS term) may not be sufficiently high to make the dissolution spontaneous. The compound becomes insoluble, e.g. CaF₂, Al₂O₃, Ca₃(PO₄)₂, ZnS, etc. (in these cases, ΔH_soln = – RT ln K_SP is a small difference between two large terms U and ΔH_soln.)

Please note that both water soluble as well as water insoluble salts have large hydration energy (CaI₂ = – 2.14 MJ mol ^–1, CaF₂ = – 6.78  MJ mol ^–1) as well as small hydration energy (KI = – 610 kJ mol ^–1_,  LiF = ^– – 1003 kJ mol ^–1).  Hence, the hydration energy (ΔH_soln) alone does not determine the solubility of compounds; Lattice energy (U) must also be considered for predicting solubilities. Both U and ΔH_soln depend upon the sizes and charges on the ions. Since U is inversely proportional to the sum of the ionic radii of cation (r_c) and anion (r_a), whereas ΔH_soln is sum of two terms each inversely proportional to the radius of the ion,

U = f₁ / (r_c + r_a)
ΔH_soln  = f₂ / r_c + f₃ / r_a

In actual practice, lattice energy is higher than solvation energy for similar sized ions and gets reduced if the size of one of the ions becomes very large. The solvation energy, on the other hand is the sum of two terms. If one of these terms is very large due to very small size of the ion, the total sum may still be large enough despite the large size of the other ion. This is shown by solubility of alkali metal halides. CsI is least soluble alkali metal iodide and LiF is least soluble alkali metal fluoride and lithium halide.

It is observed that the solubilitiy of alkali metal halides increase with increase in difference between the hydration energies of the constituent ions.

Large sized metal ion complexes can be isolated in solid state only by using an equally large counter ion. Thus, though [Ni(CN)₅]^{3 –} exists in solution, crystallization of potassium salt gives only K₂[NiCN)₄].H₂O; however, the large sized anion can be crystallized as the  [Cr(en)₃][Ni(CN)₅].1.5H₂O salt.

In nonpolar solvents, solvation energies of the ions are considerable low due to weak ion–induced dipole interactions. Hence, the lattice energy becomes higher than the solvation energy and the ions salts are generally insoluble in nonpolar solvents.

The insolubility of nonpolar solutes in polar solvents cannot be explained so obviously. The solute–solvent interactions are weak dipole – induced dipole interactions, and should be stronger than London’s forces which hold nonpolar solutes in solid state. Entropy of mixing is always favorable for dissolution. It appears that both these types of favorable factors are offset  by loss of the energy from breaking of the hydrogen bonding in solvents.