Proof for (1 + 2 + ... + n) = ½n(n+1) shown below.
A curious "Proof Without Words" solution exists for the puzzle at the back cover of Mathematical Puzzles: A Connoisseur's Collection (163 pages, 2003) by Peter Winkler. You might want to pause and solve the problem before scrolling down to see the solution.

1) Sums of Alternating Odd Numbers (PDF) by Arthur Benjamin proves 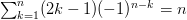 .
.
2) Putnam 2004 Problem (PDF): "Basketball star Shanille O-Keal's team statistician keeps track of the number S(N) of successful free throws she has made in her first N attempts of the season. Early in the season, S(N) was less than 80% of N, but by the end of the season, S(N) was more than 80%. Was there necessarily a moment in between when S(N) was exactly 80% of N?"
3) Roger Nelsen's homepage contains several of his publications on the subject. For example, Area of an Arbelos (PDF) — Salinon (PDF) — Euler's Triangle Inequality (PDF). A wonderful article by Roger Nelsen: Paintings, Plane Tilings and Proofs (PDF) that points out mathematical theorems implicit in tilings!
4) AM-GM inequality by Jim Wilson, University of Georgia.
5) Three proofs without words:
(A)
 ,
(B) Law of Cosines:
,
(B) Law of Cosines:
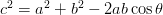 ,
and
(C)
,
and
(C)
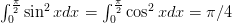 .
.
6) An article at cut-the-knot.org traces the history of Proofs Without Words.
7) Infinite Geometric Sums:
(A)
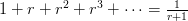 ,
and
(B)
,
and
(B)
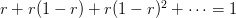 .
.
8) Proof that 1 + 2 + 3 + ... + n = n choose 2 at Wolfram.
9) Euler's arctangent property by Rex H Wu proves
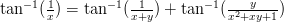 .
.
10) Geometric series:
(A)
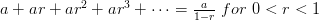 ,
and
(B)
,
and
(B)
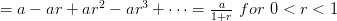 .
.
11) Proof for Integral:
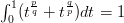 .
.
12) Lecture Notes.
13) Viviani's Theorem.
Proofs Without Words have appeared in various journals and magazines for decades now. Three books contain collections of such proofs:
1) Q.E.D.: Beauty in Mathematical Proof (64 pages, 2004) by Burkard Polster.
2) Proofs without Words: Exercises in Visual Thinking (160 pages, 1997) by Roger Nelsen.
3) Proofs without Words II: More Exercises in Visual Thinking (142 pages, 2001) by Roger Nelsen.
1) Find a "Proof Without Words" for the following problem: "Given two points A and B on the same side of a line, find point P on the line such that AP + BP is minimized." Solution.
2) Use the above insight to prove that the tangent to an ellipse always reflects a ray of light from one focus to the other. Proofs without words at MathOverflow.Net

The above solution appeared in "The Problem of Calissons" by G David and C Tomei, American Mathematical Monthly, Vol 96(5), May 1989, p. 429 - 431.


