Set 1

Chameleons

Four Pills

Pebble Piles

Rope Escape

Cake Cutting

Fox in a Hole

Cube Cutting

Patient 13

Ant Collisions

Ant in a Room
Set 2

Coin Toss Guess

Cube Problems

Truchet Tilings

Treasure Island

Magician & Balls

Six Colored Balls

Josephus Problem

Forty-Five Minutes

Thousand Prisoners

Non-Transitive Dice
Set 3

Blind Man and Cards

Breaking a Chocolate Bar

Two Dice = Nine Cards
Three Boxes and a Ruby

Absent-Minded Professor

Color of My Probabilistic Hat

Kirkman's Schoolgirl Problem

Three Boxes with Two Balls Each

Divide 100 Marbles into Two Piles

Three Heavy and Three Light Balls
Set 4

Tossing with One-Third Probability
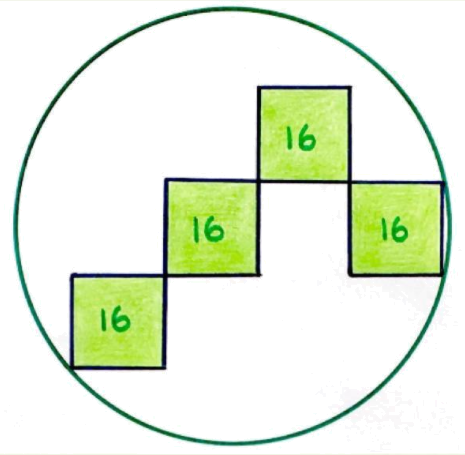
Four Squares in Circle

3-4-5 In A Triangle

11x13 Rectangle

Coins in a Row

Ants in a Circle

Fifteen Sum

Four Ships

Cap Colors

f(f(x)) = -x
Set 5

Card Shuffling

Coconut Spelling

Average Salary
Forks in a Road

Bigger or Smaller
Four Coins, Four Tumblers

Measuring Weights

Working Computer
19 Coronaviruses

Tiling With Calissons
Set 6

Loop in a Linked List

Perplexing Polynomial

Poisoned Wine Barrels

Two Eggs and a Building

Number Guessing Game

Cutting a Cake with Icing

Number Guessing Game II

Cube Cutting with Stacking

What's the Number on My Hat?

Tiling a Chessboard with Dominoes
Set 7

Tiling a Chessboard with Trominoes
Fuel Dumps on a Circular Racetrack

Red Card

My Cap Color

Square Solitaire

Twelve Coins

900 Coins

Grid Infection

Duplicate Integer

Find the Angle
Set 8

Five Card Trick

Tetrahedron in Sphere

Sum and Product

Five Circles in Square

Fast Bit Counting

Empty the Bucket

Balanced Coloring

Horses on Auction

Polya's Urn Process

Flipping Bits in a Matrix
Set 9

Rectangle with Integer Side

100 Prisoners and 100 Boxes

100 Prisoners and a Light Bulb

Firing Squad Synchronization

Four Points, Two Distinct Distances

Tumblers on a Rotating Table

Geometry With Only a Compass

Dijkstra's Self-Stabilization Protocol

Three NOT Gates from Two NOT Gates
© Copyright 2008—2023, Gurmeet Manku.

