 Imagine a cube on a flat table, tantalizingly balanced on one of its vertices such that the vertex most distant from it is vertically above it.
Imagine a cube on a flat table, tantalizingly balanced on one of its vertices such that the vertex most distant from it is vertically above it.
(a) What is the length of the shortest path an ant could take to go from the topmost vertex to the bottommost vertex?
(b) What will be the projection on the table if there is a light source right above the cube?
(c) What would be the cross-section obtained if we slice the cube along a plane parallel to the table, passing through the midpoint of the topmost and the bottommost points of the cube?
(d) Split a large 3×3×3 cube into 27 small 1×1×1 cubes. An ant can burrow through one small cube to an adjacent small cube if these two cubes share a face. Can the ant burrow through all of the 27 small cubes, visiting each small cube exactly once? Can such a sequence have the additional property that the first and the last small cube share a face?
Heard a long time ago, in 1990s.

(a) The length is √5 times the length of the edge. The solution is explained here.
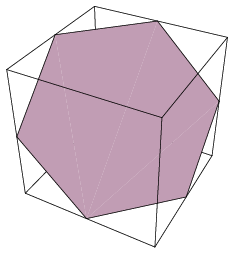
(b) A hexagon (shown on the right).
(c) A hexagon (shown below). In fact, the hexagonal cross-section allows a square to be fitted entirely inside it whose dimensions are larger than the sides of the original cube. This insight allows us to solve an old puzzle by Henry Dudeney:
(d) It is easy to find sequences of 27 distinct small cubes such that pairs of adjacent small cubes have common faces. However, it is not possible for such a sequence to enjoy the additional property that the first and the last small cubes also have a face in common.
Explanation: Color the 1×1×1 cubes either black or white such that any horizontal or vertical 3×3×1 slice looks like a chessboard. In other words, if two 1×1×1 cubes share a face, they are of opposite color. If we visit 27 small cubes in any sequence such that any pair of adjacent small cubes have common faces, then the first and the last cubes must have identical color and therefore will not have a common face.

