 One day, grandma baked a cake with a square top and dimensions 30cm x 30cm x 10cm. What is a simple strategy for cutting the cake into 9 equal pieces? The next day, grandma baked another cake with the same dimensions. This time, she put a thin layer of icing on top and on all four sides but not on the bottom. What is a simple strategy for cutting such a cake into 9 pieces such that all pieces have the same amount of cake by volume and the same amount of icing by surface area?
One day, grandma baked a cake with a square top and dimensions 30cm x 30cm x 10cm. What is a simple strategy for cutting the cake into 9 equal pieces? The next day, grandma baked another cake with the same dimensions. This time, she put a thin layer of icing on top and on all four sides but not on the bottom. What is a simple strategy for cutting such a cake into 9 pieces such that all pieces have the same amount of cake by volume and the same amount of icing by surface area?
From MathOverflow.Net discussion on interesting puzzles.
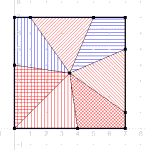
Let the dimensions of the cake with a square top be s x s x h. Let p denote the number of pieces. The problem can be solved for any values of s, h and p as follows:
Cake without icing: Pieces of size (s/p) x s x h may be carved out with p-1 cuts.
Cake with icing: Identify p points on the edges of the square top that divide its perimeter into p equal lengths. For each of these p points, slice the cake vertically (from top to bottom using a knife) along the line segment joining the center of the square top to these points. To convince yourself that the resulting pieces have equal amounts of cake (by volume) and equal amounts of icing (by surface area), please see the figure attached for p = 7. Draw additional line segments from the vertices of the square top to its center. Now the top of each piece is either a triangle or the union of two triangles. Since the area of a triangle is half the product of its base and height, it is easy to see why the p pieces divide the square equally by area.

