 Shankar chooses a number uniformly at random between 1 and 1000. Geeta has to guess the chosen number as quickly as possible. Shankar will let Geeta know whether her guess is smaller than, larger than or equal to the number. If Geeta's guess is larger than the number, Shankar replaces the number with another number chosen uniformly at random [1, 1000]. What should Geeta's strategy be?
Shankar chooses a number uniformly at random between 1 and 1000. Geeta has to guess the chosen number as quickly as possible. Shankar will let Geeta know whether her guess is smaller than, larger than or equal to the number. If Geeta's guess is larger than the number, Shankar replaces the number with another number chosen uniformly at random [1, 1000]. What should Geeta's strategy be?
Heard from Ovidiu Gheorghioiu at Google in 2007.
Geeta repeatedly guesses a fixed number n-p. When Shankar's number is greater than n-p, Geeta starts guessing n-p+1, n-p+2, and so on. Since Shankar chooses a number uniformly at random in [1, n] the probability that his number equals or exceeds n-p is p/n. So the expected number of guesses is n/p. Thereafter, Geeta has to guess p/2 numbers on average, sequentially. Minimizing the sum n/p + p/2 yields p = 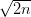 .
.

