(A) An 8x8 chessboard has had two of its diagonally opposite squares removed, leaving it with sixty-two squares. Can we tile it with 31 non-overlapping 2x1 rectangles (dominoes) such that all squares are covered?

(B) Under what circumstances would removal of two squares from an 8x8 chessboard allow such a tiling? For example, if we remove an arbitrary white square and an arbitrary black square, can the remaining board be tiled?

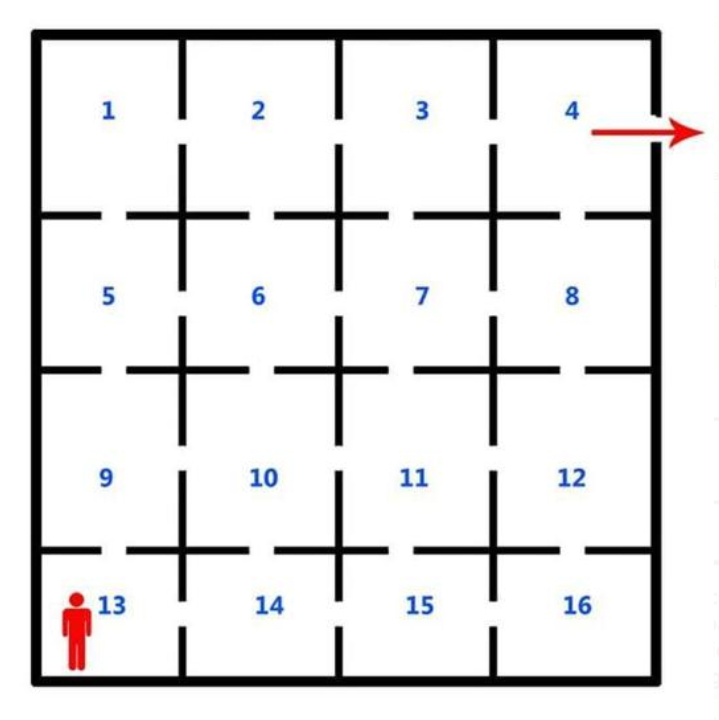(C) A hospital has 16 isolation rooms. Patient 13 is cured. He wants to pass by all other patients before leaving but he can't see the same patient twice or he will get sick again. Is that possible?

[Also known as 'Patient in Room 13 Puzzle' or 'Quarantine Puzzle'; it surfaced in 2020 after Covid-19 caught us by surprise.]

(D) In the above puzzle, imagine that we have a helicopter in one of the squares to bail us out of the hospital (instead of a door as suggested by the red arrow above). Is there a room such that if the helicopter were in that room, the puzzle would be impossible to solve?

Part (A) is the classic Mutilated Chessboard Problem posed by Martin Gardner in one of his articles in Scientific American. Part (B) has a surprising answer with an elegant mathematical proof.

(A) Both removed squares have identical color! So their removal leaves us with 30 squares of one color and 32 squares of the other color. Since a domino always covers one black and one white squares, the 62 remaining squares cannot be tiled.

(B) Removal of any white and any black square allows tiling with dominoes.

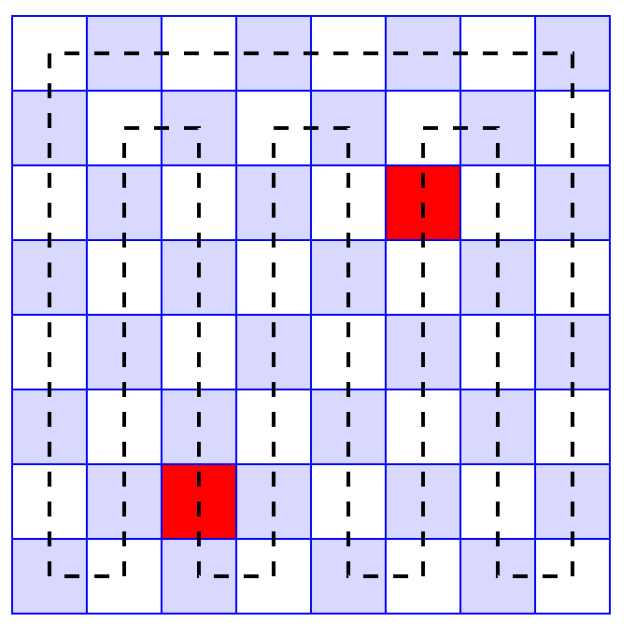Proof: Find a Hamiltonian cycle among the squares, with two squares deemed adjacent iff they share an edge. In other words, cover all squares of a chessboard using a rook without covering the same square twice, and returning to the original square. Removal of one white and one black square breaks the cycle into two paths with even lengths. A path of even length can be tiled with 2x1 dominoes because successive squares in the path share an edge.

Alternative solution (thanks to Sreeram Ramachandran at Google): The smallest rectangle that includes the excluded squares must have one side odd and the other side even. Let us call this rectangle "special". Slice the large rectangle by extending those two edges of the special rectangle that are odd in length. Then slice only that rectangle that contains the special rectangle along the two edges of the special rectangle that are even in length. Now, we have (at most) five rectangles. The rectangles other than the special rectangle have at least one side that is even. So these can be tiled. It is easy to see that the special rectangle can also be tiled.

(C) Hint: Patient number 13 may visit his own twice! :)

1) Use parity / coloring argument to show that a 10x10 board cannot be tiled with 1x4 pieces.

2) Show that if a 7x7 board is tiled with 1x3 pieces, then the untiled square must occupy one of the following 9 positions: the center, one of the four corners, or one of the central squares along the sides of the board.

Further reading:

1. A blog entry discusses the problem of tiling with dominoes with 4 squares removed.
2. Edward Dijkstra has posted a short note on the following problem: Consider tiling a chessboard with dominoes. A domino whose squares are in the same row we call a horizontal domino. We claim that the number of horizontal dominoes with a black left square and the number of horizontal dominoes with a white left square are equal. [Corollary: the number of horizontal dominoes is even.]
3. Free Chapter 1 (in PDF format) from "Across the Board: The Mathematics of Chessboard Problems" by John J. Watkins, 2004 — the chapter discusses several covering problems using dominoes and chess pieces.
4. Tilings by Federico Ardila and Richard P Stanley, Clay Public Lecture, 2004.
5. The Inquisitive Problem Solver (MAA Problem Book Series) (2002, 344 pages) by Paul Vaderlind, Richard K. Guy & Loren C. Larson discusses the general problem of rook tours with multiple forbidden squares

Solutions for Followup Problems listed above:

1) Label rows as 0, 1, ..., 9. Label columns similarly. A square in column c and row r is assigned the color (c + r) mod 4. The sum of colors covered by any 1x4 tile is 2 modulo 4. The sum of colors of 25 such tiles shall also be 2. However, the sum of colors of all 100 squares is 0.

2) Color the seven rows as 0, 1, 2, 0, 1, 2, 0. The sum of numbers covered by a tile is always divisible by 3. So the uncovered square must belong to a row labeled 0. Now repeat the same argument with 'rows' replaced by 'columns'. The intersection of these rows and columns are the 9 squares listed in the problem statement.