 An 8x8 square grid has to be covered with isosceles triangular tiles with two tiles per square. Tiles come in two colors: black and white. Such tilings are called Truchet tilings. A tiling is said to be "fine" if no two tiles sharing an edge have the same color. How many "fine" Truchet tilings are there?
An 8x8 square grid has to be covered with isosceles triangular tiles with two tiles per square. Tiles come in two colors: black and white. Such tilings are called Truchet tilings. A tiling is said to be "fine" if no two tiles sharing an edge have the same color. How many "fine" Truchet tilings are there?
From a Math competition.
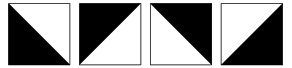
Let us solve the problem for an m by n grid. We have four choices for the top-left square as shown in the figure. For any of these choices, there are only two ways to tile the square to the right of this square. For example, if the tiles in the figure are denoted by A, B, C, D, then, A or B may be followed only by A or B, both choices being valid. Similarly, C or D may be followed by only C or D. Continuing this way, there are exactly 2n+1 ways to tile the top-most row. Now, let us tile the row below the top-most row. There are two choices for the left-most square. For each of these two choices, there is exactly one choice for the square to its right, and so on. In other words, the entire row is determined by the row above and the left-most tile in that row. So for an m x n grid, there are 2m+n possible tilings.
The tiles shown in the figure are called Truchet Tiles. Further infrormation: article at Wolfram, and Truchet tile generator.

