What is the shaded area? Can we compute it without trigonometry? Without algebra?

Heard from Himanshu Nautiyal in 2020.

Proof with Trigonometry (and Algebra):

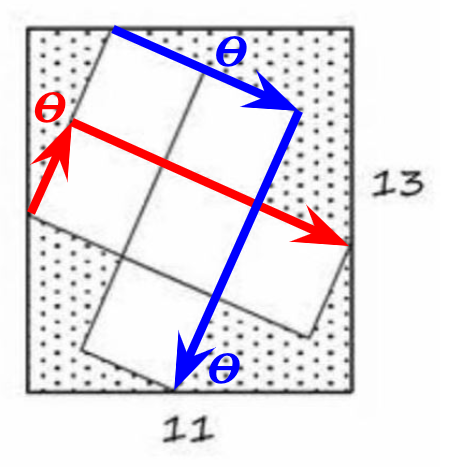
By traversing along the red and blue arrows, we get two equations in d (side of a square) and Θ (the angle by which the squares are rotated inside the 11x13 rectangle):

3d * sin Θ + 2d * cos Θ = 13
3d * sin Θ + d * cos Θ = 11

d sin Θ = 2
d cos Θ = 3

So tan Θ = 3/2. Now we can compute d² = 13, and shaded area = 11 * 13 - 6 * d² = 65.

Proof with algebra:

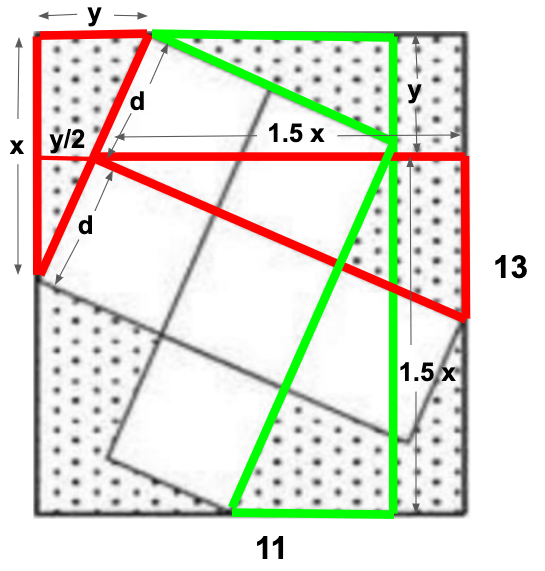
In the figure above, the two red triangles and the two green triangles are similar. Let x, y be the sides of the red triangle in the top left corner. Let 2d be its diameter. then we get two equations:

1.5x + 0.5y = 13
1.5x + 1.0y = 11

So x = 6, y = 4. Therefore, d² = 13. Shaded area = 11 * 13 - 6 * d² = 11 * 13 - 6 * 13 = 65.

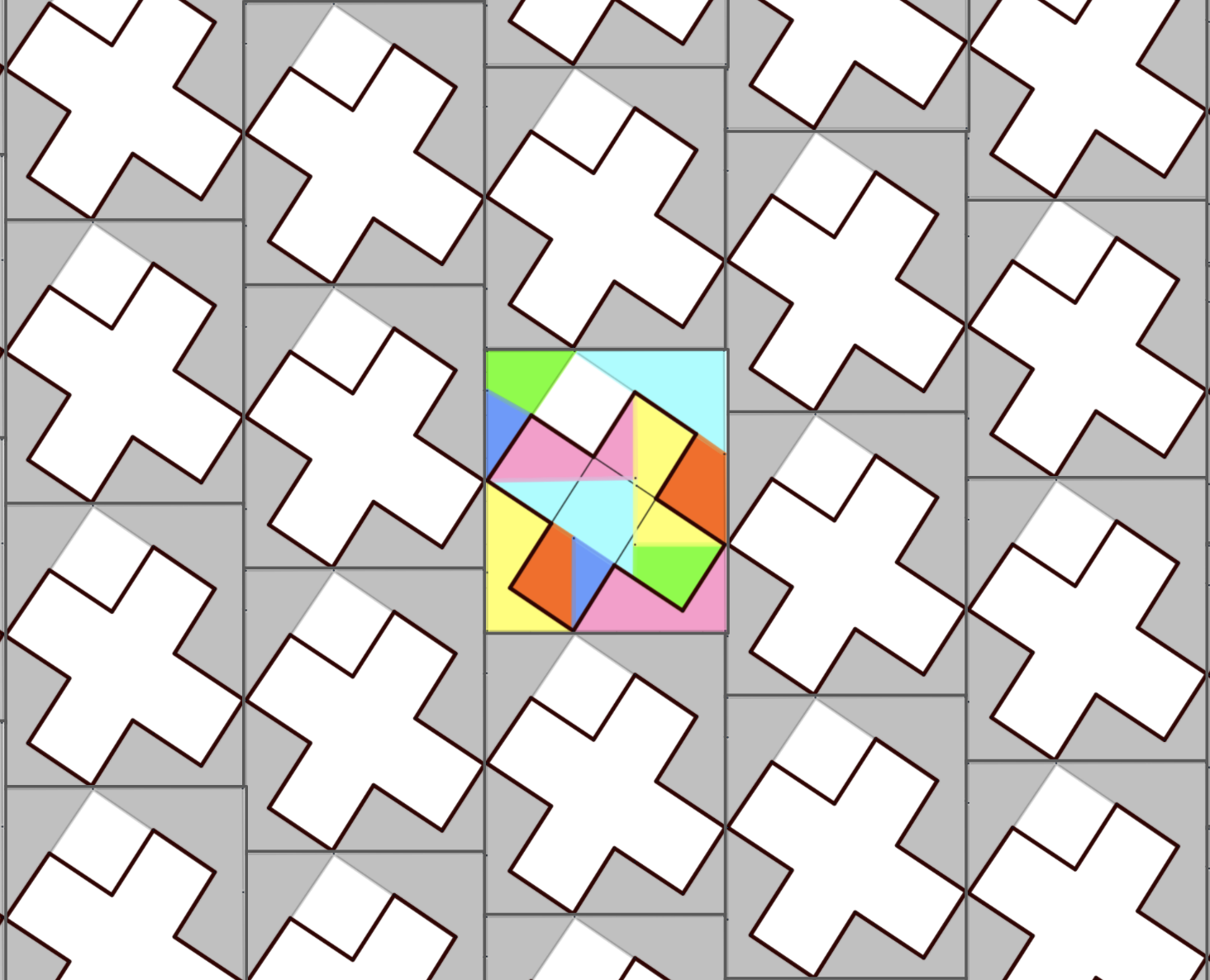
Proof Without Words! We can tile these 11x13 rectangles as shown in the pic below.

The tiling above is a composition of (a) plus signs with 5 squares each, and (b) inverted-Y signs with 6 squares each; maybe we can call them 'tuning forks'. Note that even if the horizontal lines in the figure are rotated by small angles (so that they are no longer perpendicular to the vertical lines), the tiling still holds!

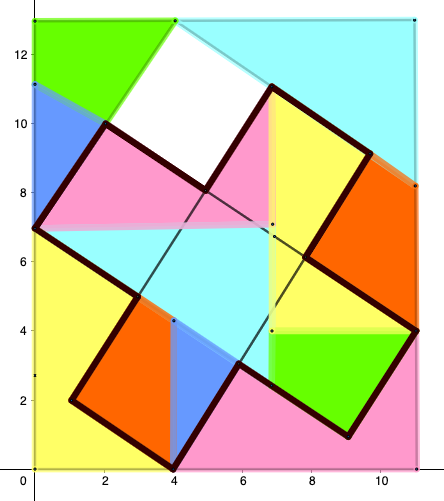
Slide each colored piece (without any rotation or reflection) into its new position by making sure that their edges and vertices along the boundaries of the plus sign overlap. The tricky part is to establish that various edges and vertices inside the plus sign are well aligned, with no two pieces overlapping each other, and no empty space left. Towards this goal, let's focus on the colorful 11x13 tile broken down into pieces like this:

Now let's convince ourselves of the following claim:

Claim: The top edge of the green figure and the bottom edge of the yellow figure are identical in length.

Proof: Consider an infinite grid of points corresponding to the vertices of the squares in the plus sign. Exactly one of these grid points lies on the topmost edge of the 11x13 figure. And exactly one of these points lies on the bottommost edge of the 11x13 figure. [A short formal proof for this claim would be helpful :) ]

Now imagine making a copy of the 11x13 grid and juxtaposing it right below the original. We see that the top edge of the green piece must be equal in length to the bottom edge of the yellow piece.

Followup: Many such puzzles have been developed by Catriona Shearer: see her Twitter feed. Catriona Shearer is a math teacher in Cambridge. Check out her fascinating puzzles! She has a 13-page file with 150+ geometric puzzles. She also wrote a book with 85 puzzles: Geometry Puzles in Felt Tip (88 pages, 2019).