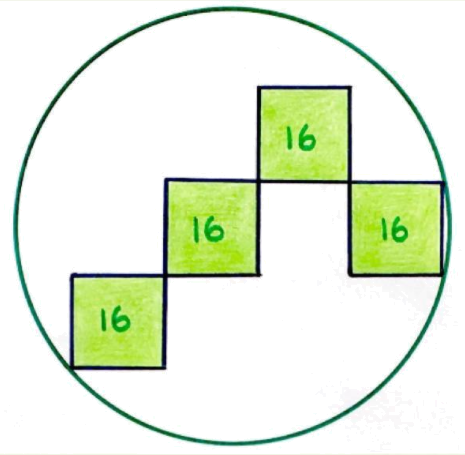
Area of each square is 16. What is the area of the circle?

Heard from an IIT Delhi classmate in April 2020. Don't remember who posted this puzzle in a group.

This problem can be solved in many different ways. For example, we may trigonometry or coordinate geometry (given three points in a circle, find its radius). However, these approaches don't unearth this elegant underlying structure of the problem: 6^2 + 7^2 = 9^2 + 2^2 = 85, which is a visual delight!

How may we arrive at the visually delightful solution below? We may reflect the four squares along the a vertical line (parallel to y-axis) passing through the center of the circle. Clearly, the horizontal lines of the grid overlap. We have to establish that the vertical lines also overlap. Is there a simple argument for that?