We have 30 bags with 30 coins each (for a total of 900 coins). One of the bags has counterfeit coins. It is not known whether the counterfeit coins are lighter or heavier than genuine coins. How many times do we have to use a weighing scale to identify which bag has counterfeit coins and whether the counterfeit coins are lighter or heavier?

From Mohit Aron (IIT Delhi classmate; founder of Nutanix and Cohesity), June 2020.

Let's divide the 30 bags into 3 groups named A, B and C. Let bags 1-10 be called A1 thru A10; let bags 11-20 be called B1 thru B10; let bags 21-30 be called C1 thru C10.

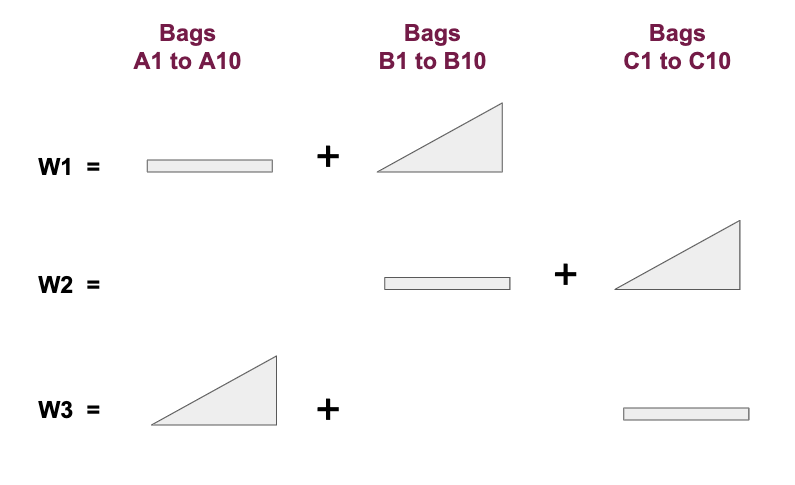
Compute three weights as follows:

W1 = Bar(A) + Triangle(B) + None(C)
W2 = None(A) + Bar(B) + Triangle(C)
W3 = Triangle(A) + None(B) + Bar(C)

where

Bar(X) is defined as "1 coin from every bag in group X".
Triangle(X) is defined as "i coins from the i-th bag in group X".
None(X) is defined as "zero coins from bags in group X".

Sort the three weights in ascending order. The weights cannot be identical. Only three configurations of sorted weights are possible: ⟨ W_low, W_low, W_high ⟩ or ⟨ W_low, W_high, W_high ⟩ or ⟨ W_low, W_medium, W_high ⟩, where W_low, W_medium, W_high are distinct. Let's analyze these configurations one by one.

Case 1: ⟨ W_low, W_low, W_high ⟩: In this case, the counterfeit bag is lighter; the index of the counterfeit bag is 1; the counterfeit bag belongs to the group that's missing in W_high. In other words, if W_high = Bar(X) + Triangle(Y) + None(Z), then group Z contains the counterfeit bag.

Case 2: ⟨ W_low, W_high, W_high ⟩: In this case, the conterfeit bag is heavier; the index of the counterfeit bag is 1; it belongs to the group that's missing in W_low. In other words, if W_low = Bar(X) + Triangle(Y) + None(Z), then group Z contains the counterfeit bag.

Case 3: ⟨ W_low, W_medium, W_high ⟩: In this case, all three weights are distinct.

Claim 1: Index of counterfeit bag cannot be 1.

Proof: When index = 1, either the lowest two weights must be equal or the largest two weights must be equal, which contradicts W_low < W_medium < W_high.

Claim 2: Let W_medium = Bar(X) + Triangle(Y) + None(Z). The counterfeit bag belongs to group X.

Proof: Let's assume that Claim 2 is not true. Then the counterfeit bag must be in Group Y or Group Z.

If Group Y has the counterfeit bag, then W_medium must be the largest or smallest weight (depending upon whether the counterfeit bag is heavier or lighter); W_medium cannot be in the middle, a contradiction.

Similarly, if Group Z has the counterfeit bag, W_medium must be the largest or smallest weight (depending upon whether the counterfeit bag is lighter or heavier); W_medium cannot be in the middle, a contradiction.

We are now ready to identify the fake bag for Case 3 (when all three weights are distinct):

Which group has the counterfeit bag? If W_middle = Bar(X) + Triangle(Y) + None(Z), then group X contains the counterfeit coin.

Is the counterfeit bag lighter or heavier? That depends on which sum — W_low or W_high — contains Triangle(X). If W_low has Triangle(X), then the counterfeit bag is lighter. If W_high has Triangle(X), then the counterfeit bag is heavier.

What is the index of the counterfeit bag? If the counterfeit bag is lighter, its index is (W_high - W_low) / (W_high - W_medium). If the counterfeit bag is heavier, its index is (W_high - W_low) / (W_medium - W_low).