Inside an equilateral triangle lies a point that is at distances 3, 4 and 5, respectively, from the three vertices of the triangle. What is the area of the triangle?

Heard from Cosmin Negruseri in 2020. Later, I discovered it at Cut The Knot: here

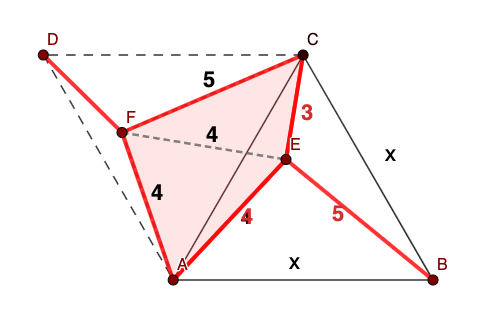
Let the triangle be ABC as shown in the diagram below.

Our goal is to compute A(3, 4, x) + A(3, 5, x) + A(4, 5, x), where function A denotes "area of".

Rotate the equilateral triangle by 60 degrees in the anti-clockwise direction while keeping A fixed. Now let's focus on (4, 5, x) in the new equilateral triangle, along with (3, 4, x) in the original equilateral triangle. Note that A(3, 4, x) + A(4, 5, x) = A(3, 4, 5) + A(4, 4, 4). This is a key observation. Writing two additional similar equations and summing them all, we get 2 * [A(3, 4, x) + A(4, 5, x) + A(3, 5, x)] = 3 * A(3, 4, 5) + A(3, 3, 3) + A(4, 4, 4) + A(5, 5, 5).