A perfect in-shuffle of a deck of 52 cards is defined as follows. The deck is cut in half followed by interleaving of the two piles. So if the cards were labeled 0, 1, 2, ..., 51, the new sequence is 0, 26, 1, 27, 2, 28, ... With repeated in-shuffles, shall we ever get back the original order? In how many iterations?

(a) Two monkeys are typing capital letters (A-Z) randomly. The first stops typing when the word COCONUT appears as seven successive letters. The second stops typing when TUNOCOC appears; TUNOCOC is simply COCONUT spelt backwards. Which monkey is expected to type more?

(b) A monkey is typing capital letters (A-Z) randomly. Two squirrels observe the sequence of letters thus generated. The first squirrel wins if COCONUT appears (as seven successive letters) before TUNOCOC. The second squirrel appears if TUNOCOC appears before COCONUT. Which squirrel is more likely to win?

Four honest and hard-working computer engineers are sipping coffee at Starbucks. They wish to compute their average salary. However, nobody is willing to reveal an iota of information about his/her own salary to anybody else. How do they do it?

A traveler has to pass tests of increasing difficulty to meet an Eastern mystical master. For the first test, he meets a pair of twins at a fork in the road: one path leads to the jungle, the other to the mystic. One of the twins always says the truth, the other always lies. What yes/no question should you ask one of the twins to determine the path that goes to the mystic? For the second test, the traveler encounters a second fork in the road. Again, one path leads to the jungle, the other to the mystic. This time, there are three look-alike brothers: one always tells the truth, the second always lies but the third sometimes tells the truth and sometimes lies. What two Yes/No questions should the traveler ask two of the brothers to determine the path to the mystic? Each question is answered by only the brother it is posed to. For the second question, the traveler may choose the brother and the question depending upon the answer to the first question.

Alice writes two distinct real numbers between 0 and 1 on two chits of paper and places them in two different envelopes. Bob selects one of the envelopes randomly to inspect it. He then has to declare whether the number he sees is the bigger or smaller of the two. Is there any way he can expect to be correct more than half the times Alice plays this game with him?

Alice and Bob take turns to play a game with four coins on the corners of a square table covered by four identical tumblers. At her turn, Alice rotates the table in the blink of an eye by a random amount and presents it to Bob. Then Bob gets to choose any two tumblers to reveal the coins underneath; for each of the revealed coins, he may choose its configuration: heads up or tails up; he then covers both the coins that he just inspected with tumblers. At any moment, if all four coins become either four heads or four tails, Bob wins! Does Bob have a deterministic winning strategy? If not, why?

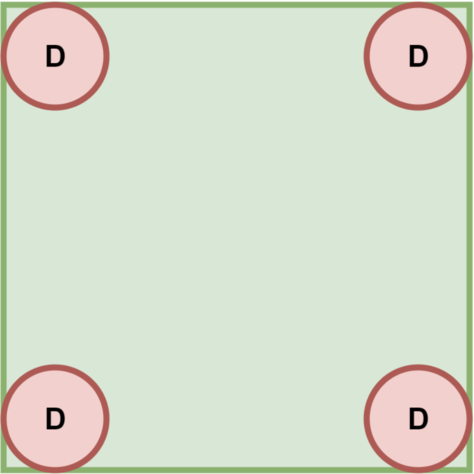
Followup: What if we have 6 tumblers on a hexagonal table and Bob gets to pick any 4 tumblers in each turn? Does Bob have a deterministic winning strategy? [Generalize the solution to n = 2k tumblers at the corners of an n-gon.]

(a) Customers at a grocer's shop always want an integral number pounds of wheat, between 1 pound and 40 pounds. The grocer prefers to measure wheat in exactly one weighing with a beam balance. What is the least number of weights he needs?

(b) Customers come to a pawn shop with antiques. An antique always weighs an integral number of pounds, somewhere between 1 pound and 80 pounds. The owner of the pawn shop is free to do as many weighings as necessary to ascertain the unknown integral weight by using a beam balance. What is the least number of weights he needs?

A room has n computers, less than half of which are damaged, others are good. It is possible to query a computer about the status of any computer. A damaged computer could give wrong answers. The goal is to discover a good computer in as few queries as possible.

Imagine a circular ring of 19 cells. Each cell has a coronavirus inside it: either active or inactive. Scientists have developed a special drug that can target a specific cell (of your choice). When the drug hits its target, it affects not only the targeted cell but also its 2 neighbors! The effect of the drug on these three cells is unusual: if the coronavirus in that cell was active, it become inactive; if the coronavirus in that cell wsa inactive, it become active! In other words, one dose of a drug toggles the state of 3 coronaviruses in 3 adjacent cells.

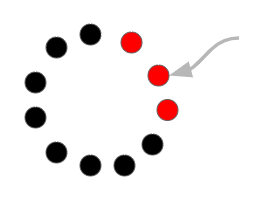
If all coronaviruses are active in the initial state, is there a sequence of drug targets so that all coronaviruses become inactive at the same time? What is the length of the smallest such sequence?

A large regular hexagon is cut out of a triangular grid and tiled with diamonds (pairs of triangles glued together along an edge). Diamonds come in three varieties, depending on orientation; prove that precisely the same number of each variety must appear in the tiling.